音高
音高
音高是指让我们能够演奏音乐旋律的声音品质。初级的神经科学教材往往将音高等同于频率。然而,大多数现实世界的声音包含许多频率成分,但只有一个清晰的音高或根本没有音高。《听觉神经科学》第3章描述了决定音高的声音特征,概述了西方古典音乐中对待音高的方式,并描述了大脑如何通过提取声音周期性的物理线索来创建主观的音高知觉。以下一系列网页提供了与该章节配套的补充材料。
Melodies and Timbre
Melodies and Timbre
Many different sounds have the same pitch - you can play the same melody with a flute or with a clarinet or with a horn. Here, you can hear the same melody played on three computer-generated instruments.
The melodies in these examples share the same sequence of pitches, and have about the same sound level. The property of sounds that is different between them is called 'timbre' - the timbre of the flute is different from that of the clarinet and from that of the horn.
Here are the spectra of the three versions:
Flute 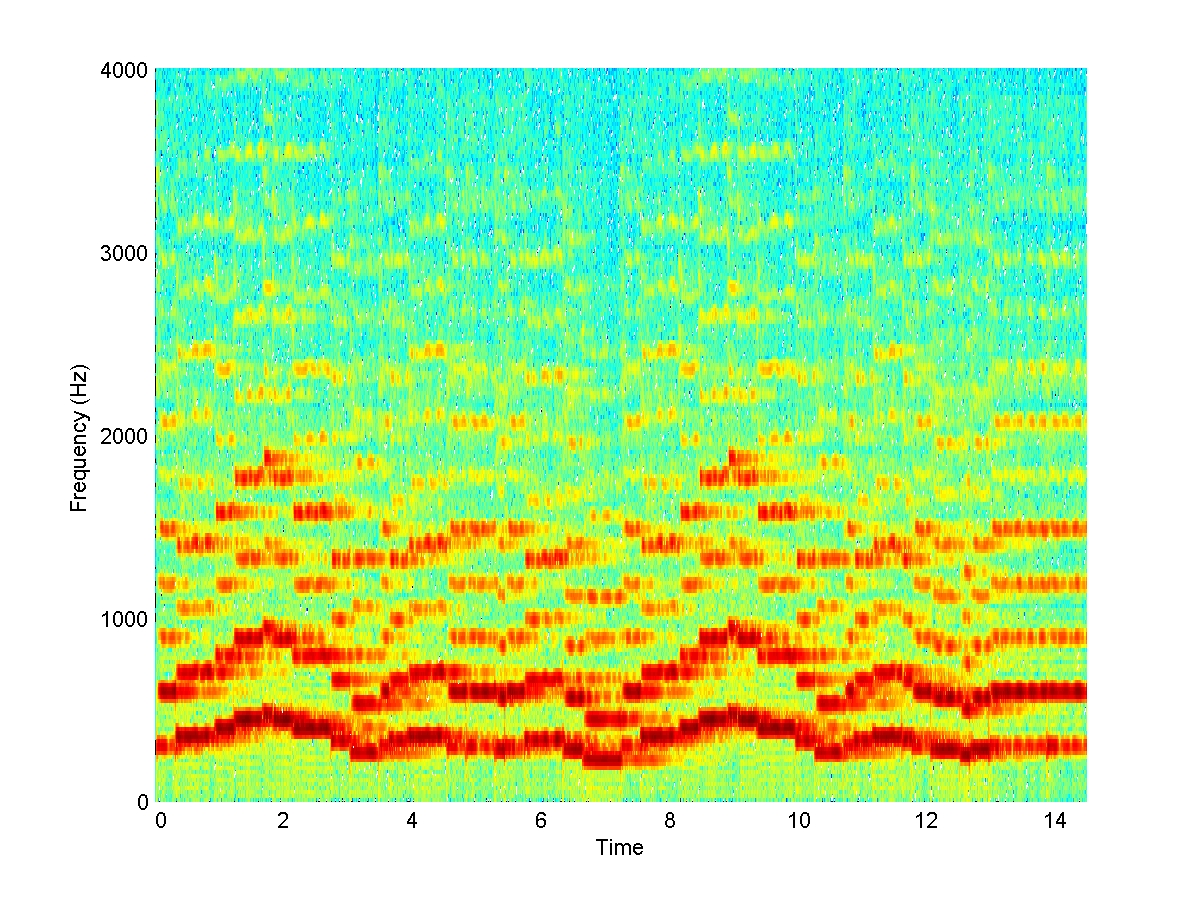
Oboe 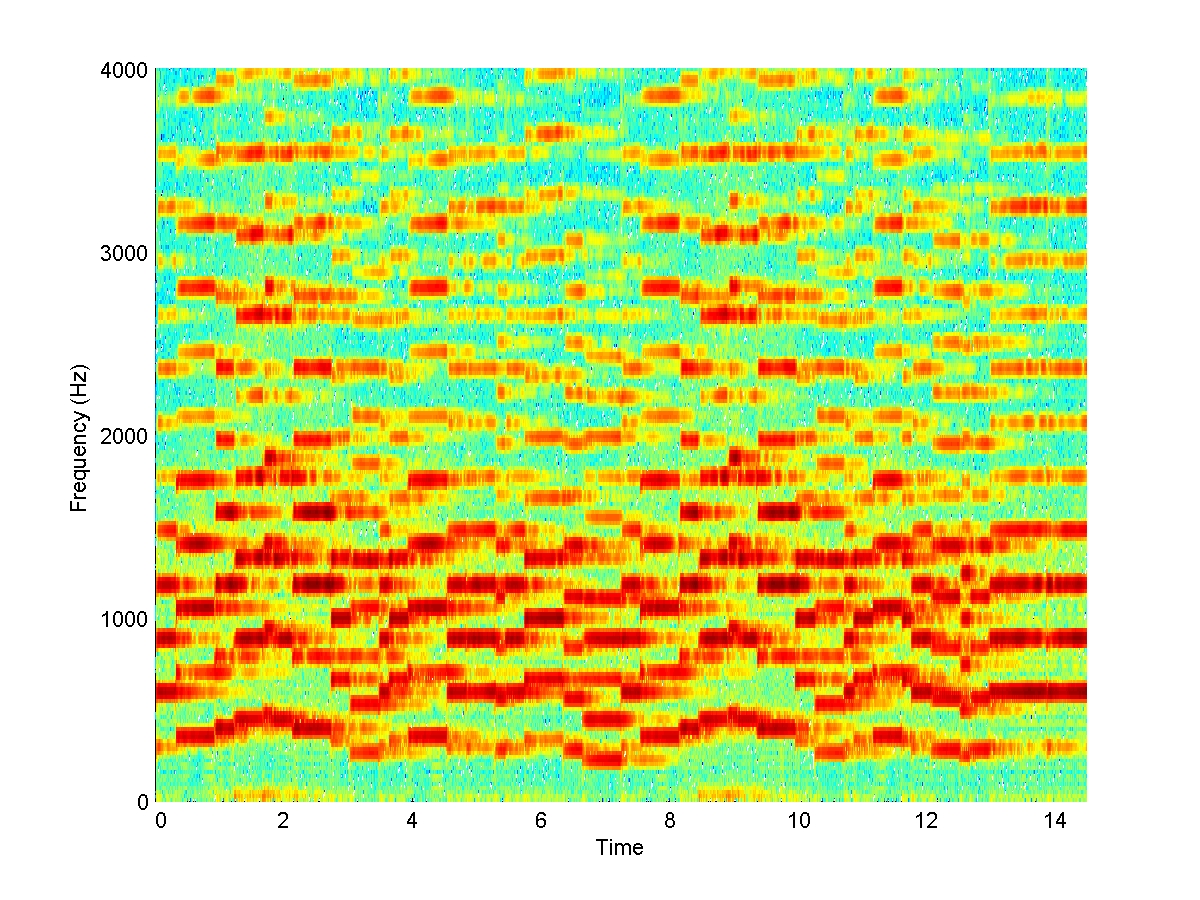
Horn
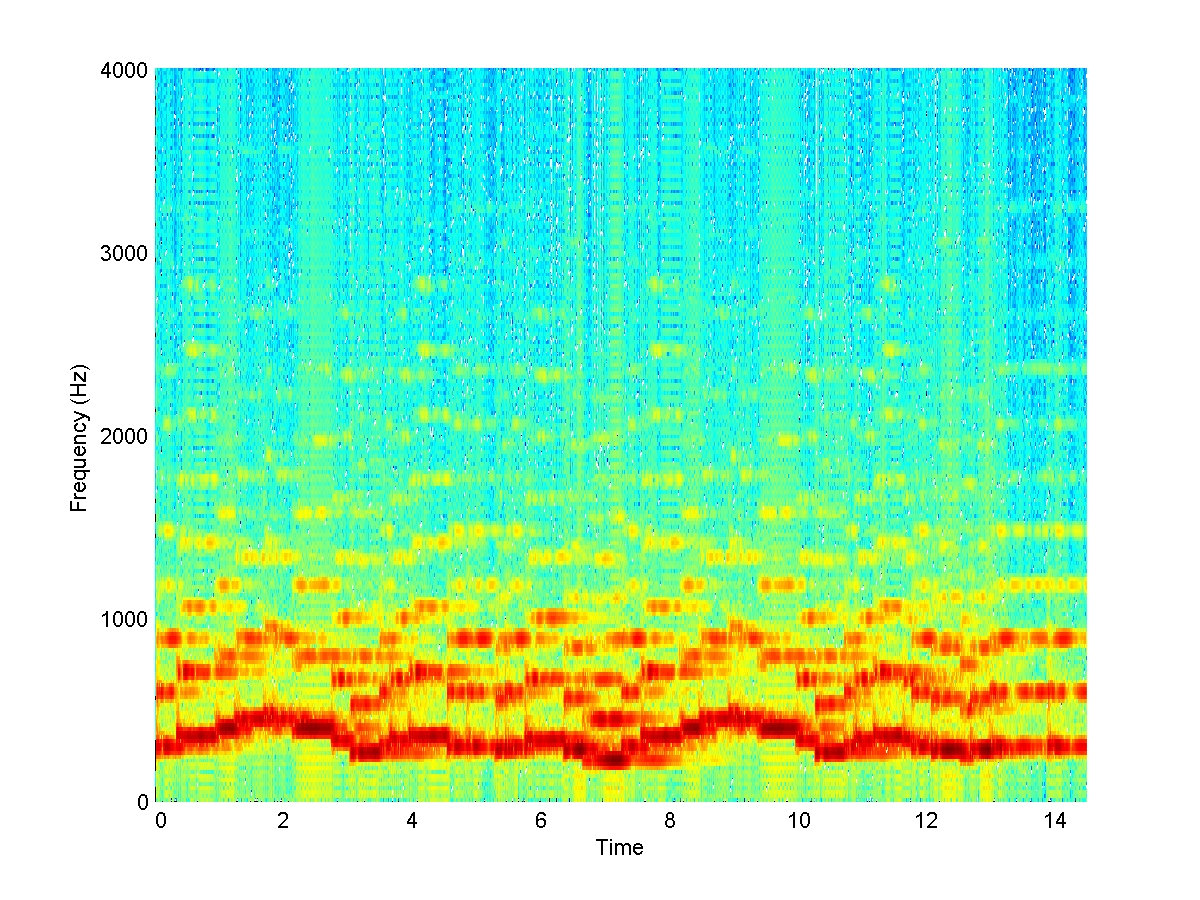
Note the large differences between the spectra, as well as the similarities. The sequence of pitches is to a large extent apparent in the line of the fundamental (the lowest red band). However, the number and relative strengths of the higher harmonics vary substantially between the three instruments, resulting in their unique timbre.
How many repetitions are required to produce pitch?
How many repetitions are required to produce pitch?
The main determinant of pitch is sound periodicity. A sound is periodic when it is composed of consecutive repetitions of a single short segment (the 'period'). The following figure (fig. 3.1 "Auditory Neuroscience") shows examples of periodic sounds:
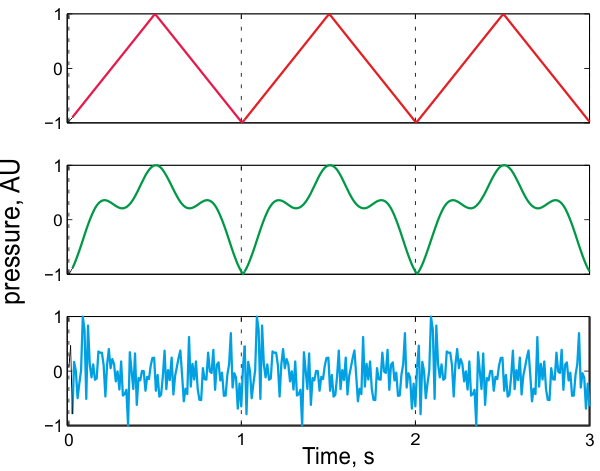
Only a small number of repetitions of a period are required to generate the perception of pitch. The following sounds are all composed of the same period, which repeats itself a different number of times in each example. Each such sound is repeated a few times.
A single repeat results in no pitch sensation at all - there is nothing periodic:
With eight repeats, a clear pitch is heard:
Find out yourself what is the minimal number of repeats that is necessary in order to hear pitch!
2 Repeats:
3 Repeats:
4 Repeats:
6 Repeats:
8 Repeats:
Pitch matching
Pitch matching
Pitch is defined by its perceptual qualities, and therefore has to be determined by the judgment of human listeners. By convention, we use the pitch evoked by pure tones as a yardstick with respect to which we judge the pitch evoked by other sounds. In practical terms, this is performed by matching experiments: A periodic sound whose pitch we want to measure is presented alternatively with a pure tone. Listeners are asked to change the frequency of the pure tone until it evokes the same pitch as the periodic sound. The frequency of the matching pure tone then serves as a quantitative measure of the pitch of the tested periodic sound. In such experiments, subjects most often set the pure tone so that its period is equal to the period of the test sound. In the demonstrations below, the sound to be tested is played four times alternately with a pure tone. The test sound is the same at all repetitions, but the period of the pure tone changes from repetition to repetition: it is the same as the period of the test sound in the first repetition, shorter(higher pitch) in the second, longer (lower pitch) in the third, and is again the same as that of the test sound in the last repetition.
Here is the demonstration, with the test sound being a cosine-phase harmonic complex at 400 Hz:
Here is the demonstration, with the test sound being an Iterated Repeated Noise (IRN) with 4 iterations, again at 400 Hz:
Now you are ready to try pitch matching by yourself. In the following gadget, you can select the type of pitch-evoking sound and try to match it by moving the slider.
Click "Start" to hear a pure tone and a complex sound, played in alternation. Adjust the horizontal slider to change the frequency of the tone until it matches that of the complex sound.
The range of periods that evoke pitch
The range of periods that evoke pitch
Regular click trains at a rate of less than about 40 Hz sound like individual regular events, perhaps a bit like machine-gun fire. Click trains with rates faster than about 40 Hz merge into a continuous "buzz", where the pitch of the buzz depends on the click rate: the faster the rate, the higher the pitch.
The two sound examples below illustrates this. The first example consists of a click train, where the rate of the clicks doubles every 3 seconds. During the first 3 seconds, the rate of the clicks is about 10.7 Hz, then it increases to 21.4 Hz, 43 Hz, 86 Hz, 172 Hz, 344 Hz, 689 Hz, 1378 Hz, 2756 Hz, and 5512 Hz. Clear pitch emerges between 43 Hz and 86 Hz, although at 86 Hz there is still 'flutter', and full smoothness of the resulting percept occurs only at rates of a few hundreds Hz.
The second example consists of clicks which are presented initially at a rate of about 10 Hz. The rate then continuously speeds up, to a rate of 10,000 Hz, and then slows down again. At the beginning and the end you will hear a rapid train of individual clicks, but in the middle you hear a buzz of rapidly rising, then falling, pitch. The sequence is illustrated in the figure below.
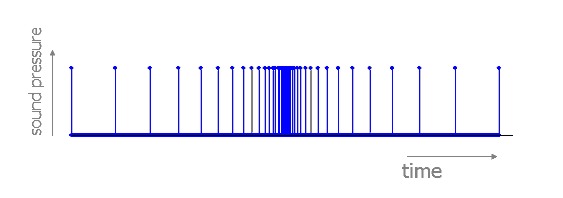
Vowels are not strictly periodic
Vowels are not strictly periodic
One of the most important classes of sounds that have pitch in the natural environment are voiced speech sounds. However, like many other naturally-produced sounds, these sounds are not strictly periodic. In spite of this, they produce a strong sense of pitch. Sounds that are not strictly periodic but that do evoke pitch are in fact the rule, rather than the exception.
Here is a naturally-produced human vowel:
Elliot and Theunissen addressed this question by calculating the "modulation spectra" of speech as shown here:
The spectrogram of the vowel is presented on the left below, while on the right three consecutive periods are shown superimposed. Each of the periods has a length of about 6.75 ms - the pitch here is about 150 Hz. The periods have been extracted from around time 50 ms in the spectrogram. Note the small, but continuously present, changes in the sound, which can be observed both by following it period by period (right) and at the longer time scale, of 100s of ms, which can be followed in the spectrogram.
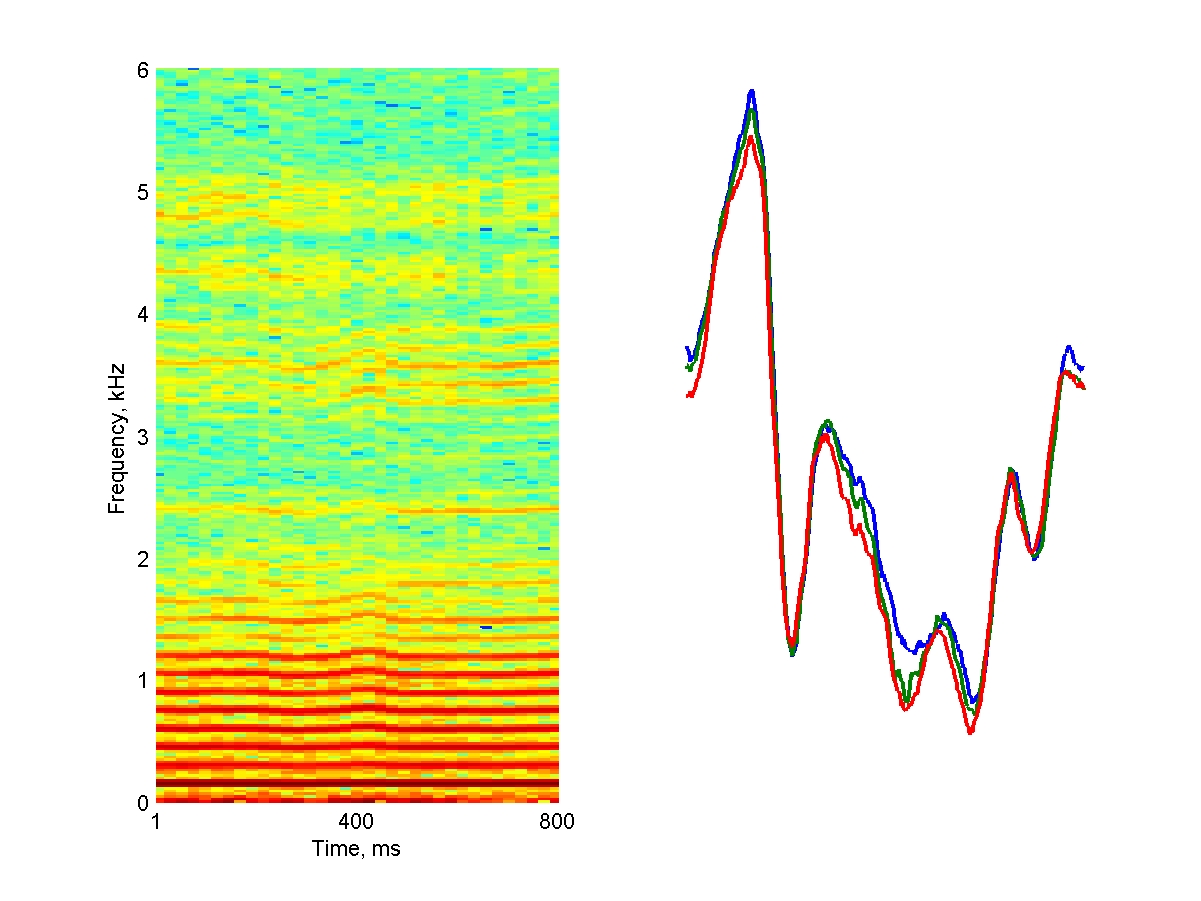
These micromodulations are crucial for the natural quality of the sound. When the micromodulations are removed, making the sound strictly periodic, it becomes buzzy and artificial, losing much of its speech quality:
Additional information about modulations in speech can be found in 'speech as a "modulated signal"'.
Missing fundamentals. Periodicity and Pitch
Missing fundamentals. Periodicity and Pitch
As explained in the section on modes of vibration. most natural sound sources will not emit pure tones, but sounds composed of many, often harmonically related frequencies. Now, some texts on hearing will tell you that the pitch of a sound is "related to the sound's frequency", but if a sound contains many (possibly harmonically related) frequencies then it may not be at all obvious which of the sound's frequencies determines the pitch.
Take the following example. Here we have a simple melody played in pure tones.
Pure tones
And here we have the same melody played using "complex" tones containing sine waves with the same fundamental frequency as well as 9 additional "higher harmonics" (multiples of the fundamental).
Harmonics 1-10
Spectrograms of these sounds are shown in the picture below.
Now it should be obvious that the melodies (and hence the pitches) are the same, even if the overall frequency content, and therefore the "timbre", of these sounds is different. These two sounds do however share the same fundamental frequency: the second souns is literally the sum of the first one plus the contributions of the higher harmonics. So it may be tempting to think that it is the presence of the fundamental frequency that determines the pitch.
The curious thing is that you can take this fundamental frequency out, leaving only the higher harmonics, and the pitch still remains the same. This is what we have done in the following sound (in fact, for good measure, we took out not just the fundamental but the next two harmonics too, so that only harmonics 4 to 10 are left; when listening, turn down the volume to reduce the harmonic distortions produced by the speakers, which would reintroduce the lower harmonics!).
Harmonics 4-10
The first melody and the third melody have no frequency components in common. You can verify that on the spectograms shown here below to the left. Nevertheless they are 'the same' in that they have the same sequence of pitches.
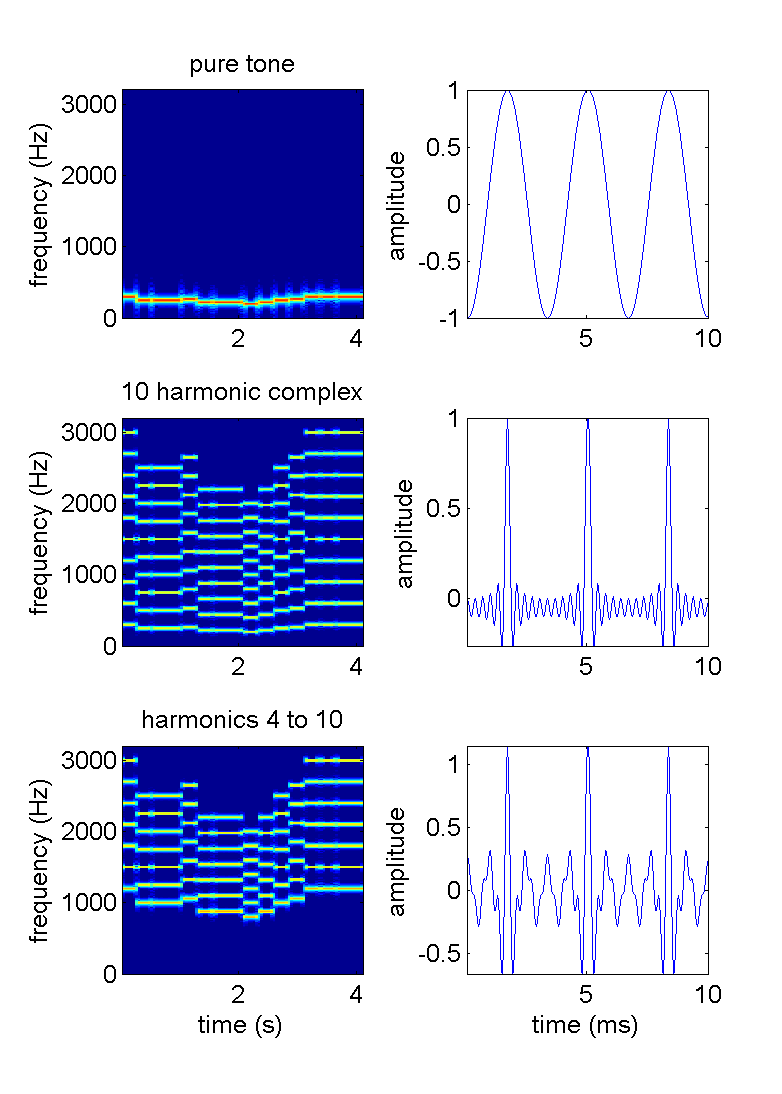
"Missing fundamental" stimuli, like the third melody, argue strongly against a simple frequency place code in the cochlea as the main cue for perceived pitch. A more reliable cue is the sound's periodicity. The panels on the right in the figure above zoom in on a 10 ms long sound snippet during the first note for each of the melodies here. This note has a fundamental of 300 Hz, so there are three whole cycles in 10 ms. This 300 Hz periodicity (identical wave form patterns repeating themselves at a rate of 300 such patterns per second) is something that the first note in all three of the examples here clearly have in common, even though the corresponding sound in the third melody does not contain a 300 Hz (Fourier) frequency component. It has the right periodicity because all its frequency components have a 300 Hz periodicity, but they do not share any longer period.
Why Missing Fundamental Stimuli are Counterintuitive
Why Missing Fundamental Stimuli are Counterintuitive
The fact that tone complexes with missing fundamentals can be perceived to have a pitch that is below their lowest frequency component can have counterintuitive consequences.
Consider the tone sequence shown in the spectrogram here:
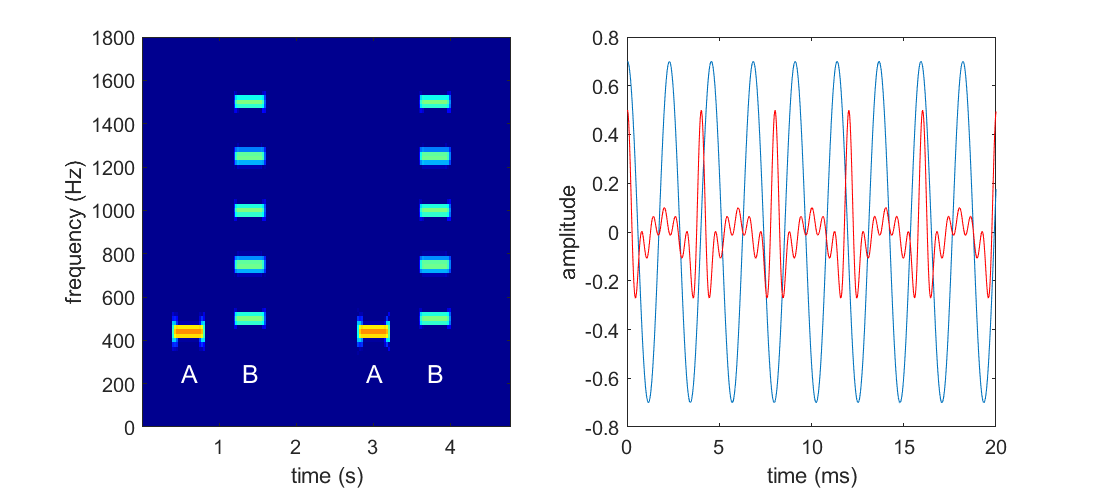
A 440 Hz pure tone (labelled "A") alternates with a tone complex containing frequencies 500, 750, 100, 1250 and 1500 Hz (labelled "B"). All frequencies in B are above the frequencies in A, but nevertheless when you listen to these stimuli you may find that B sounds lower because the pitch of B is perceived to be that of a missing 250 Hz fundamental.
Note also that most people find it quite hard to judge what the relative pitches of the A and B sounds really are because their timbre is so different. That just highlights that pitch is complicated, and that it would be naive to think that it is a simple mapping of tonotopic, cochlear place coding to perception.
The panel on the right shows the waveforms of the two sounds, with the "A" sound in blue and the "B" sound in red. Note that the A sound has a pattern that repeats every 1000/440=2.27 ms, as you might expect, but the B sound has has a pattern that repeats only every 4 ms because its harmonics beat at the fundamental. Thus, the A sound "cycles faster" than the B sound, and "timing theories of pitch" would predict that it should therefore have a higher pitch.
Or here is another example:
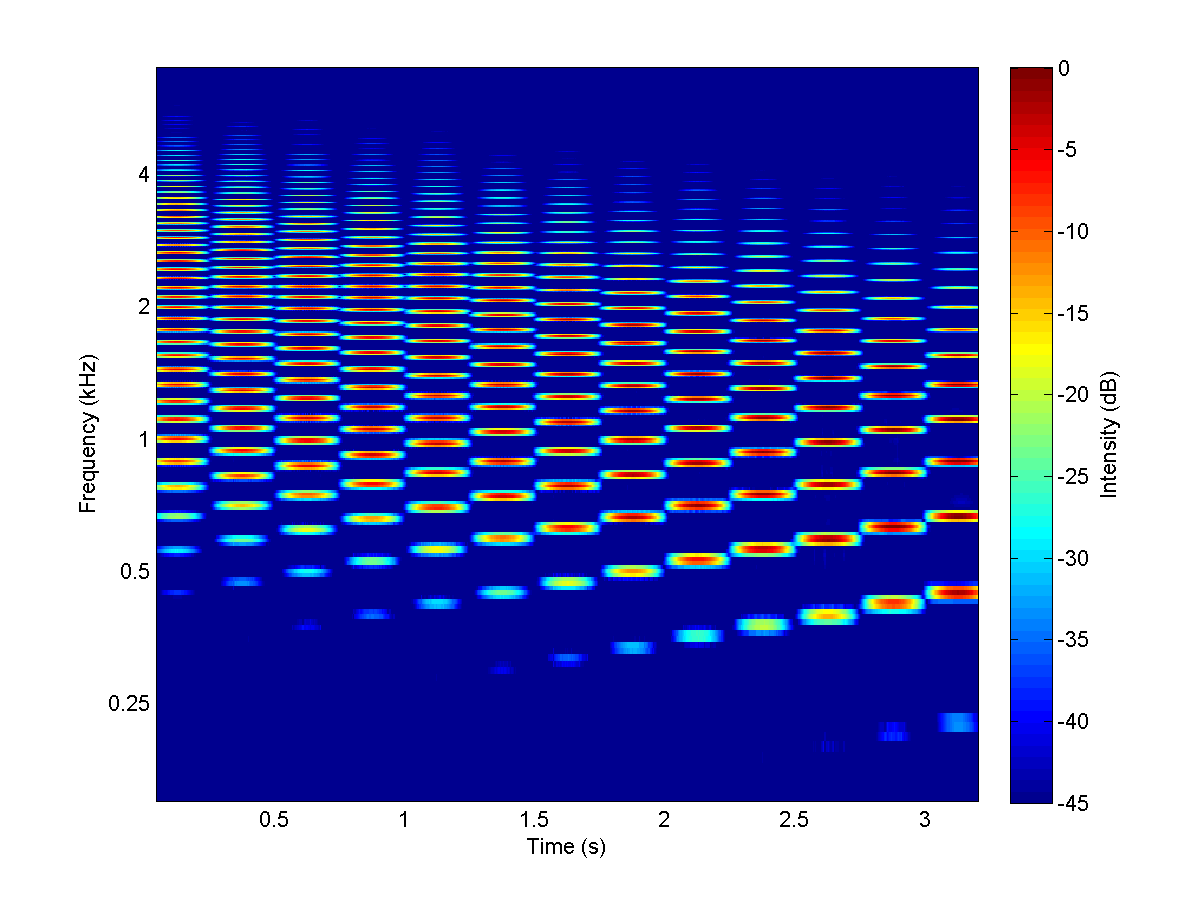
The sounds in this spectrogram are harmonic complexes with a fundamental frequency that rises from 110 to 220 Hz in semitone steps. So the pitch should be rising from the musical notes A2 to A3. But the harmonic complexes have been bandpass filtered to be 3.5 octaves wide with the lower edge of their passband falling from 880 Hz to 440 Hz. So the frequency components become increasingly lower, but the pitch should get higher, at least in as far as harmonic structure is the dominant pitch cue. Do the pitches sound falling or rising to you?
非周期性声音引发的音高
非周期性声音引发的音高
以下是三种非严格周期的声音,它们能够唤起音高感。关于这些声音的详细讨论可以在这本书的音高章节中找到。
这些声音都近似周期性,它们的频谱具有近似周期结构,类似于严格周期声音的谐波结构。在每种情况下,都存在一个明确的周期。如果将声音按照该周期进行移动,它最接近未移动的版本。
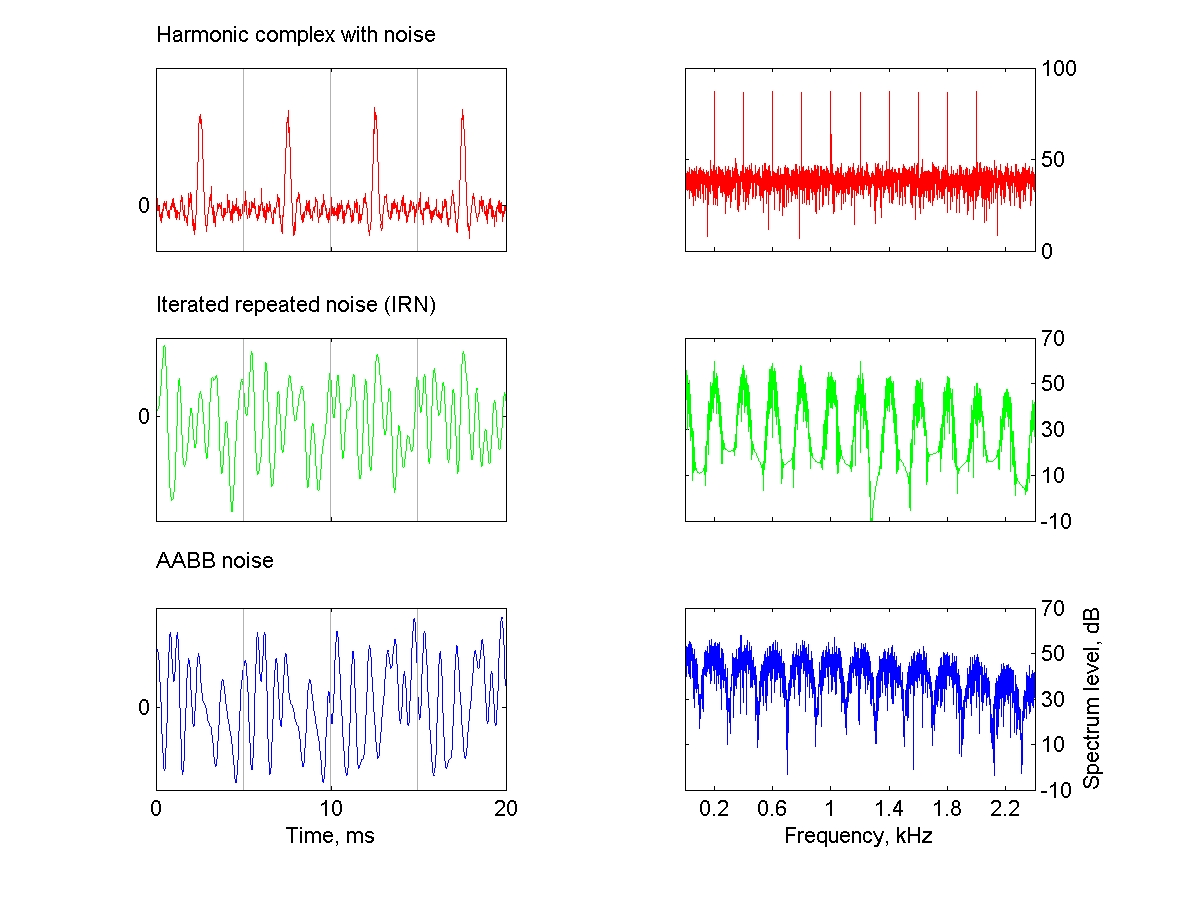
Harmonic complex with noise
Iterated repeated noise (IRN)
AABB noise
周期声音必须具有谐波结构
周期声音必须具有谐波结构
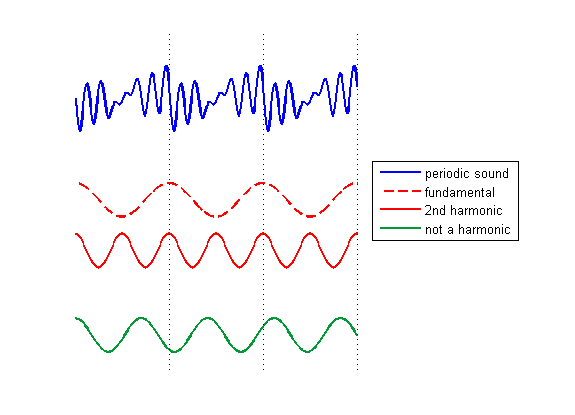
周期声音(具有重复"动机"的波形,如上图所示的蓝色曲线)的傅里叶谱必定完全由声音的"谐波"组成。谐波是周期为某个基本周期的整数倍的正弦波。上图中的红线是蓝线的"余弦相位"谐波。在考虑傅里叶谱时,我们想象蓝线由许多像红线和绿线这样的正弦波之和组成,其中我们可以根据需要调整正弦波的相位和振幅。需要注意的重要一点是,无论我们如何调整绿线的相位和振幅,它都无法成为组成蓝线所需的混合物的一部分。原因是:比较波形在周期内相同点的值,例如通过比较由点线标记的点的值。红线每个周期总是在相同的位置贡献相同的值(例如,在由灰线标记的周期上总是达到最大值)。相反,绿线无法将整数个周期"适应"到基本周期内,因此它对波的每个周期的贡献将不同,这将破坏波的周期性。因此,绿线不能是周期蓝色声波的傅里叶分量。任何其他具有周期不是声音基本周期的谐波的正弦波也不能成为其傅里叶分量。
三阶谐波复合音的音高
三阶谐波复合音的音高
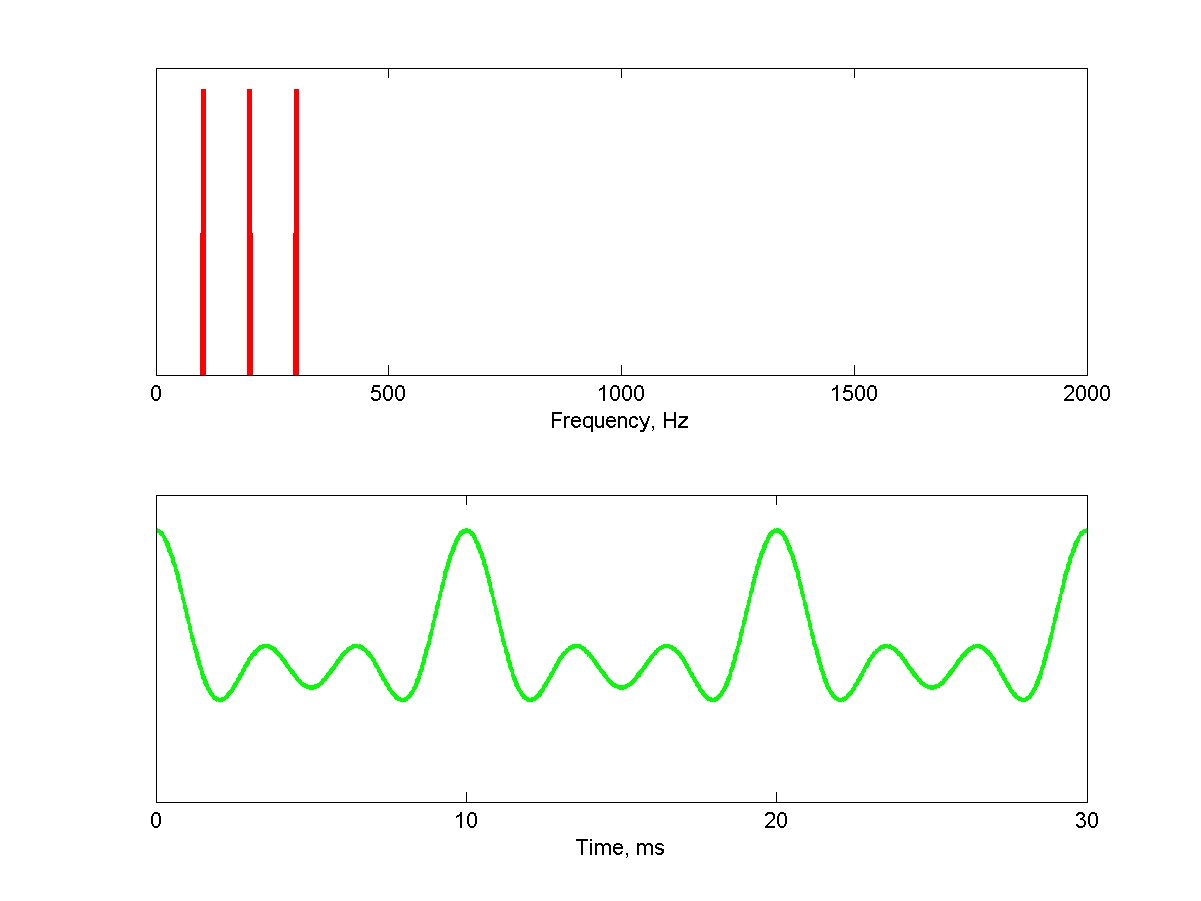
由三个连续谐波组成的谐波复合物是最简单的周期性声音之一。它们的周期性由谐波之间的间距决定。下面是一个由100 Hz的第1个谐波(基频)、第2个谐波和第3个谐波组成的复合物。顶部面板显示了该声音的频谱,底部面板显示了一个30毫秒长的波形片段,由三个周期组成(100 Hz对应10毫秒的周期)。这个声音的音高非常明显:
当这些复合物由非常高谐波次数的谐波构成时,它们仍然具有相同的周期性。然而,它们的音高不再与它们的周期性相对应。下面是一个由100 Hz的第21、22和23个谐波组成的复合物(注意:为了避免产生能再生基频的谐波失真,您应该降低计算机扬声器的音量!):
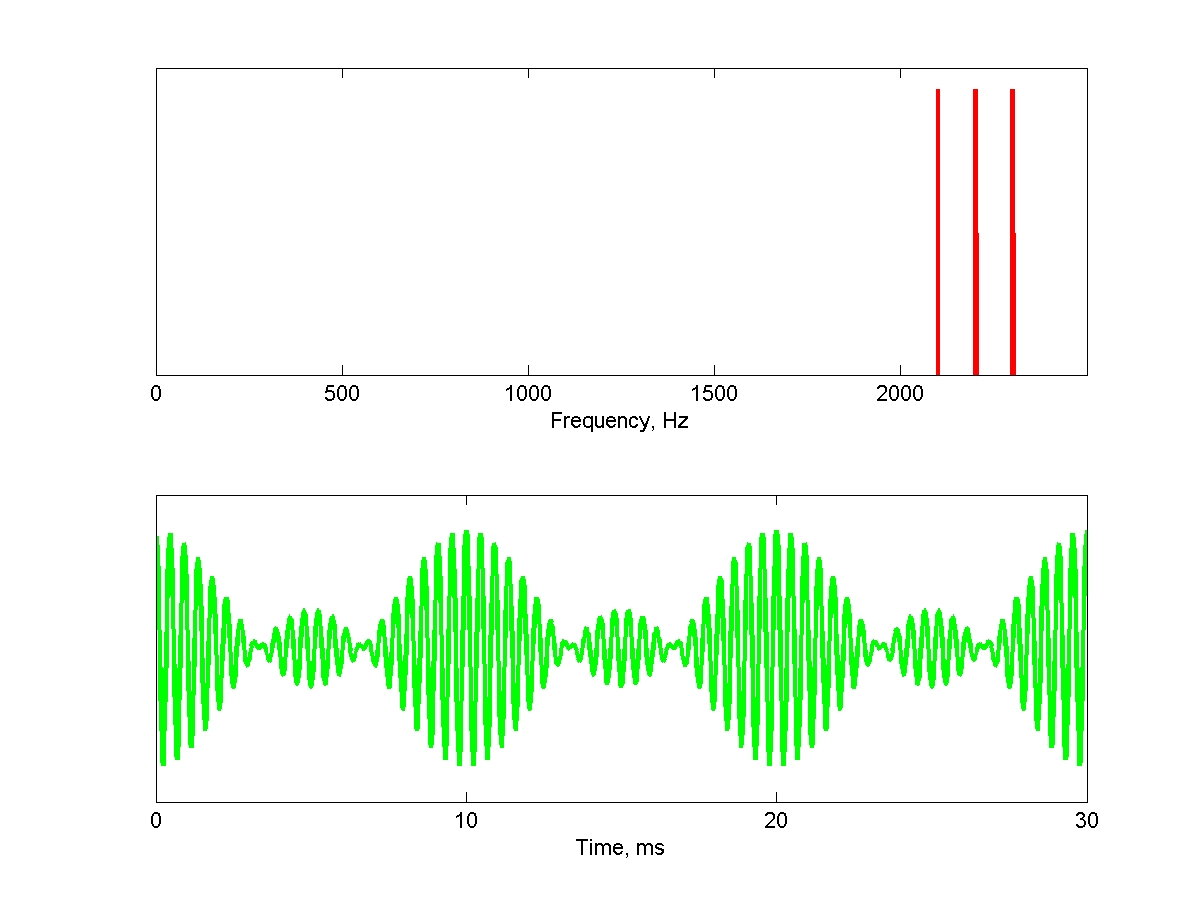
对于周期性音高何时出现,这种演示将推动低质量计算机扬声器的能力。这些扬声器难以再现几百赫兹以下的声音,但在几千赫兹的频率上会产生严重的谐波失真。因此,要听到具有较低谐波次数的示例,您需要使用较高的音量,而要避免由谐波失真再生基频,您需要使用较低的音量。
Harmonics 1 to 3
Harmonics 2 to 4
Harmonics 3 to 5
Harmonics 4 to 6
Harmonics 5 to 7
Harmonics 7 to 9
Harmonics 9 to 11
Harmonics 11 to 13
Harmonics 13 to 15
Harmonics 17 to 19
Harmonics 21 to 23
声音的周期性和包络的周期性
声音的周期性和包络的周期性
在大多数情况下,音高是由声音波形的周期性决定的。然而,有些声音具有其他更微妙的周期性。在某些情况下,这些周期性可能确定音高,但在其他情况下则不会。这里所指的微妙周期性是指包络的周期性。
请看下面的图。这个声音(蓝色)是通过许多谐波的和声生成的,这些谐波在“余弦相位”下达到峰值-这是一种复杂的方式,即所有谐波在音高周期的开始时同时达到峰值。生成的波形非常尖峭,但在峰值附近具有逐渐增大的快速波动,而在两个峰值之间的中点附近波动最小。可以想象一种“包络”-一种在每个时间点测量声音波形的总体能量的正波形。包络(在这里使用“希尔伯特变换”计算-这只是一个次要问题)用灰色绘制出来。
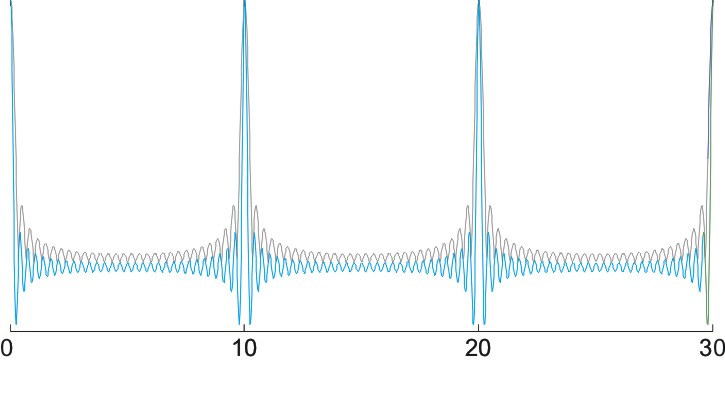
Sound
Envelope
现在,请观察下面的图。这个声音是用相同的谐波生成的,只是每隔一个谐波处于余弦相位,而另一半谐波处于“正弦相位”-这意味着它们在音高周期的开始处有一个向上的零交叉点(记住,谐波是正弦波!)。与前一个声音相比,这个声音在音高周期内有两个相似形状但极性相反的“事件”。然而,它的周期性与前一个声音完全相同,且引发的音高也相同。然而,包络在每个音高周期内现在有两个峰值,在使用相同的方法计算时,其周期是波形的一半。因此,它的音高是原来的两倍(在这种情况下是200 Hz而不是100 Hz)。
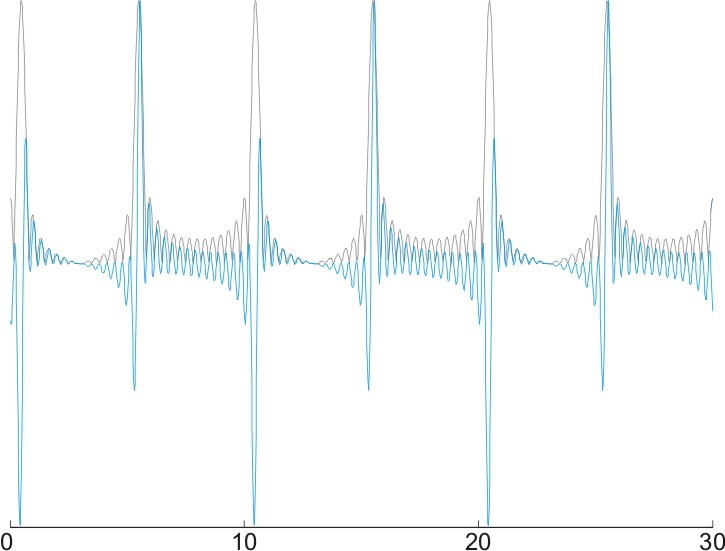
Sound
Envelope
当我们研究神经元对周期性声音的响应时,这一点非常重要。神经元可能对包络而不是声音本身作出反应。这种神经元无法对音高进行编码,即使它们对周期性敏感,因为它们对交替相位的谐波复合体给出的答案不正确。
单共振峰元音与变化的音高
单共振峰元音与变化的音高
这个声音说明了Cariani和Delgutte(1996)在听觉神经纤维的音高编码研究中使用的一种声音。它被称为单共振峰元音,因为其频谱包络在频率上只有一个峰值(元音有多个这样的“共振峰”-参见第4章)。请参阅书中的图3-9。
下面是两个连续的周期,一个周期来自声音的开头(绿色),另一个周期来自声音的中间(橙色):
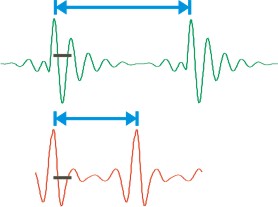
蓝色箭头跨越一个周期的声音(你可以看到连续两个周期是多么相似)。在声音的中间,周期大约是开头的一半。
灰色条表示每个周期的“细结构”的一个循环,它由共振峰频率决定。与音高周期不同,它们本质上彼此相等。
因此,这个声音的音高在大约一个八度范围内变化(在声音的中间比起声音的开头和结尾高一倍),但其共振峰频率保持不变。因此,其音色个持续时间内保持不变。
西方音乐中音符的基频
西方音乐中音符的基频
《听觉神经科学》第三章详细讨论了西方音乐中使用的音高间隔。为了方便起见,从 http://www.phy.mtu.edu/~suits/notefreqs.html.上复制了一个等律音阶的基频表格。
按照惯例,A4 = 440 Hz。
音符之间由"半音"间隔分开。每个八度有12个半音,基频呈对数间隔分布,所以每个音符的基频是前一个频率的2(1/12) = 1.0595倍。
波长值假设声速为345 m/s。
("中央C"是C4)
| Note | Frequency (Hz) | Wavelength (cm) |
|---|---|---|
| C0 | 16.35 | 2109.89 |
| C#0/Db0 | 17.32 | 1991.47 |
| D0 | 18.35 | 1879.69 |
| D#0/Eb0 | 19.45 | 1770. |
| E0 | 20.60 | 1670. |
| F0 | 21.83 | 1580. |
| F#0/Gb0 | 23.12 | 1490. |
| G0 | 24.50 | 1400. |
| G#0/Ab0 | 25.96 | 1320. |
| A0 | 27.50 | 1250. |
| A#0/Bb0 | 29.14 | 1180. |
| B0 | 30.87 | 1110. |
| C1 | 32.70 | 1050. |
| C#1/Db1 | 34.65 | 996. |
| D1 | 36.71 | 940. |
| D#1/Eb1 | 38.89 | 887. |
| E1 | 41.20 | 837. |
| F1 | 43.65 | 790. |
| F#1/Gb1 | 46.25 | 746. |
| G1 | 49.00 | 704. |
| G#1/Ab1 | 51.91 | 665. |
| A1 | 55.00 | 627. |
| A#1/Bb1 | 58.27 | 592. |
| B1 | 61.74 | 559. |
| C2 | 65.41 | 527. |
| C#2/Db2 | 69.30 | 498. |
| D2 | 73.42 | 470. |
| D#2/Eb2 | 77.78 | 444. |
| E2 | 82.41 | 419. |
| F2 | 87.31 | 395. |
| F#2/Gb2 | 92.50 | 373. |
| G2 | 98.00 | 352. |
| G#2/Ab2 | 103.83 | 332. |
| A2 | 110.00 | 314. |
| A#2/Bb2 | 116.54 | 296. |
| B2 | 123.47 | 279. |
| C3 | 130.81 | 264. |
| C#3/Db3 | 138.59 | 249. |
| D3 | 146.83 | 235. |
| D#3/Eb3 | 155.56 | 222. |
| E3 | 164.81 | 209. |
| F3 | 174.61 | 198. |
| F#3/Gb3 | 185.00 | 186. |
| G3 | 196.00 | 176. |
| G#3/Ab3 | 207.65 | 166. |
| A3 | 220.00 | 157. |
| A#3/Bb3 | 233.08 | 148. |
| B3 | 246.94 | 140. |
| C4 | 261.63 | 132. |
| C#4/Db4 | 277.18 | 124. |
| D4 | 293.66 | 117. |
| D#4/Eb4 | 311.13 | 111. |
| E4 | 329.63 | 105. |
| F4 | 349.23 | 98.8 |
| F#4/Gb4 | 369.99 | 93.2 |
| G4 | 392.00 | 88.0 |
| G#4/Ab4 | 415.30 | 83.1 |
| A4 | 440.00 | 78.4 |
| A#4/Bb4 | 466.16 | 74.0 |
| B4 | 493.88 | 69.9 |
| C5 | 523.25 | 65.9 |
| C#5/Db5 | 554.37 | 62.2 |
| D5 | 587.33 | 58.7 |
| D#5/Eb5 | 622.25 | 55.4 |
| E5 | 659.26 | 52.3 |
| F5 | 698.46 | 49.4 |
| F#5/Gb5 | 739.99 | 46.6 |
| G5 | 783.99 | 44.0 |
| G#5/Ab5 | 830.61 | 41.5 |
| A5 | 880.00 | 39.2 |
| A#5/Bb5 | 932.33 | 37.0 |
| B5 | 987.77 | 34.9 |
| C6 | 1046.50 | 33.0 |
| C#6/Db6 | 1108.73 | 31.1 |
| D6 | 1174.66 | 29.4 |
| D#6/Eb6 | 1244.51 | 27.7 |
| E6 | 1318.51 | 26.2 |
| F6 | 1396.91 | 24.7 |
| F#6/Gb6 | 1479.98 | 23.3 |
| G6 | 1567.98 | 22.0 |
| G#6/Ab6 | 1661.22 | 20.8 |
| A6 | 1760.00 | 19.6 |
| A#6/Bb6 | 1864.66 | 18.5 |
| B6 | 1975.53 | 17.5 |
| C7 | 2093.00 | 16.5 |
| C#7/Db7 | 2217.46 | 15.6 |
| D7 | 2349.32 | 14.7 |
| D#7/Eb7 | 2489.02 | 13.9 |
| E7 | 2637.02 | 13.1 |
| F7 | 2793.83 | 12.3 |
| F#7/Gb7 | 2959.96 | 11.7 |
| G7 | 3135.96 | 11.0 |
| G#7/Ab7 | 3322.44 | 10.4 |
| A7 | 3520.00 | 9.8 |
| A#7/Bb7 | 3729.31 | 9.3 |
| B7 | 3951.07 | 8.7 |
| C8 | 4186.01 | 8.2 |
| C#8/Db8 | 4434.92 | 7.8 |
| D8 | 4698.64 | 7.3 |
| D#8/Eb8 | 4978.03 | 6.9 |
Context Dependence of Pitch: Shepard Tone Hysteresis
Context Dependence of Pitch: Shepard Tone Hysteresis
"Shepard" tones are superpositions of pure tone components, in which the Nth tone has a frequency one octave above the (N-1)th tone (unlike you typical complex tone or harmonic complex, where the Nth tone is (N-1) octaves above a lowest common "fundamental" frequency.)
Shepard tones are interesting in that their pitch can be somewhat ambiguous, and this ambiguity can lead to curious perceptual phenomena. One phenomenon is that Shepard tones can be used to create continuous sounds known as "Shepard-Risset glissandos" which appear to be either continuously rising or falling in pitch. Another phenomenon is that the perceived pitch of Shepard tones can depend on the context in which they are presented. Here we present one demonstration of this context dependent pitch ambiguity that was studied in this paper by the group of Daniel Pressnitzer.
First consider this pair of Shepard tones. The components of the second complex are exactly half way between the components of the first complex. One could therefore perceive the two tone sequence either as a rising or a falling pitch step. There is no single "correct" answer. You may hear this as "clearly rising", while others may hear it as "falling" in pitch, and others may just be uncertain about the pitch change direction.
Listen to the tone pair a few times and make up your mind about what you think it sounds like before you move on:
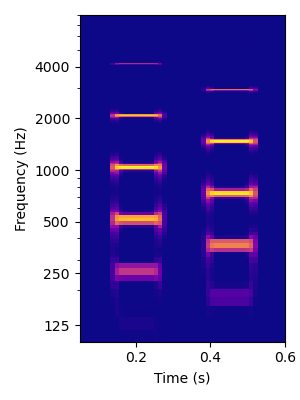
Now consider two sequences, each consisting of six Shepard tone pairs. One distinguishing feature of the sequence labelled "Falling" from the one labelled "Rising" is that the first pair of the Falling sequence could be seen as either a small down step or a very large up step, and the reverse is true for the first pair of the Rising sequence. It appears that our brains will go with the "smaller step" interpretation, and pretty much all listeners will hear the first pair in the Failling sequence as being a small down step in pitch. The Falling sequence then continues with more pairs in which the downward pitch step becomes gradually larger. Similarly, the Rising sequence comprises increasinglingly larger up steps in pitch.
Now here comes the punchline: both sequences end in a pair in which the pitch step is exactly half an octave, and which is therefore intrinsically ambiguous. The last (6th) pair in both sequences is identical, and it is exactly the same tone pair that you have already encountered in isolation above. However, depending on whether this pair is presented in a context of either a falling or a rising sequence of pitch steps, the brain hears this sound pair very differently, as either "clearly falling" or "clearly rising" in pitch.
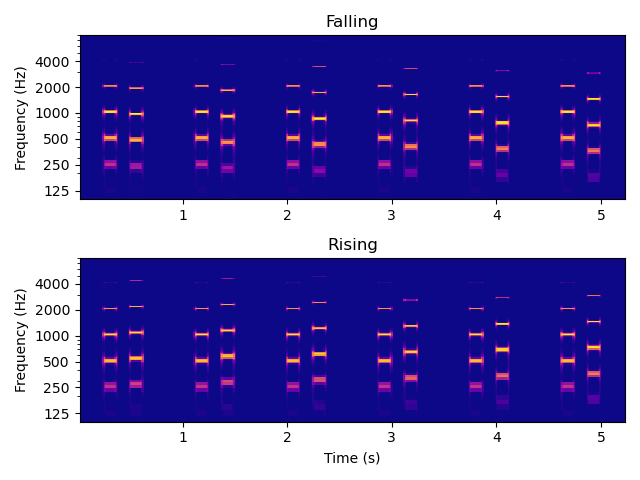
Falling:
Rising:
The idea that the same sounds can evoke very different pitches depending on the context in which they are encountered is challenging for people who, perhaps through musical training or otherwise, have been brought up to think that the perceived pitch of a sound should conform in an "objective" manner to some physical properties of the sound or the sound source, such as a fundamental resonance frequency. In reality, the pitch of a sound, perhaps not unlike the color of an object, is a subjective perceptual quality which is created by our brains, and while it is informed by the physical attributes of a given sound, it is not wholly determined by it.
讲座:复杂声音的皮层表示
讲座:复杂声音的皮层表示
这个视频片段展示了 Jan Schnupp在2011年4月18日在哈罗盖特举行的英国神经科学协会会议上关于复杂声音的皮层表示的演讲。
[swf file="http://howyourbrainworks.net/jan/JanBNApitchTalk.flv"]